Jean-Paul Vignault a mis au point pour pst-solides3d quelques remarquables options permettant de travailler avec les solides géométriques. En voici quelques illustrations.
Les fichiers sont ici :
http://manuel.luque.free.fr/cuboctahedron/cuboctahedron.zip
ou
Pour créer un cuboctaèdre avec pst-solides3d, il existe une méthode très simple :
à partir d'un cube, on utilise l'option [trunc=all] de pst-solides3d avec comme coefficient [trunccoeff=0.5] pour découper les 8 coins du cube.
On rendra la représentation un peu plus attrayante avec les faces transparentes [opacity=0.5] et en permettant de voir l'intérieur [hollow]. Le choix des couleurs est laissé à l'appréciation de chacun.
Une des particularités du cuboctaèdre est que le rayon de la sphère circonscrite a la même longueur que les arêtes.
On sait aussi, que l'on peut considérer le cuboctaèdre comme l'intersection d'un octaèdre et d'un cube,
https://mathcurve.com/polyedres/cuboctaedre/cuboctaedre.shtml
On peut facilement mettre en évidence les intersections des faces avec pst-solides3d.
Maintenant, si l'on se tourne vers Wikipedia :
https://fr.wikipedia.org/wiki/Cubocta%C3%A8dre
« Les arêtes d’un cuboctaèdre forment quatre hexagones réguliers. Si le cuboctaèdre est coupé dans le plan d’un de ces hexagones, chaque moitié est une coupole hexagonale (ou coupole triangulaire) »
Ce découpage est aisé à faire avec pst-solides3d. Voici le coupole supérieure :
Un peu plus loin dans la même page, on lit :
« Si les moitiés sont replacées ensemble avec une rotation, alors ces triangles rencontrent les triangles et les carrés rencontrent les carrés, le résultat est un autre solide de Johnson, l'orthobicoupole hexagonale. »
Ici aussi, la manipulation se fait sans trop de difficulté avec pst-solides3d. Mais pour faire la rotation j'ai utilisé une commande que j'avais écrite et illustrée ici :
https://pstricks.blogspot.com/2013/02/rotation-3d-autour-dun-axe.html
https://pstricks.blogspot.com/2013/02/rotation-3d-autour-dun-axe-quelconque.html
Le voici avec l'option [affinage=all]
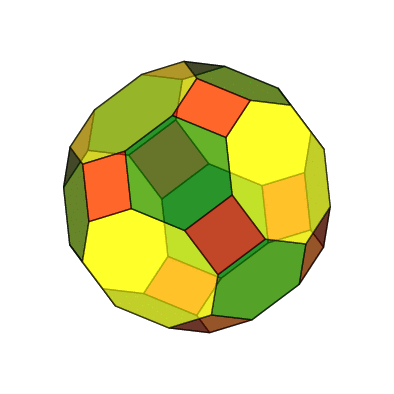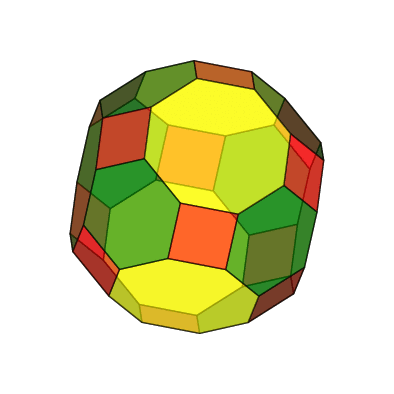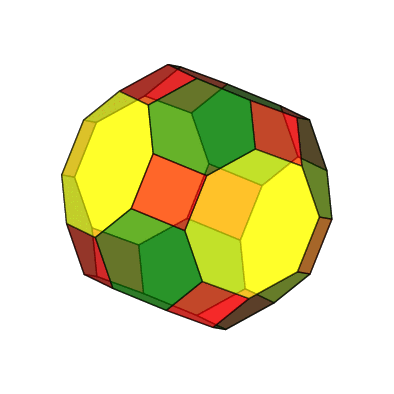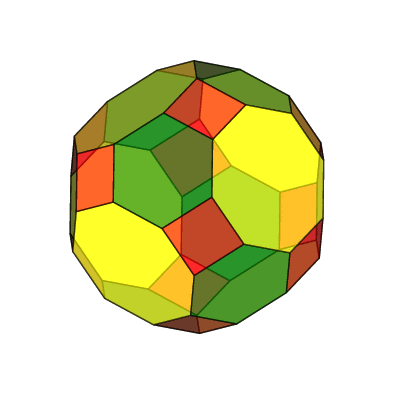
Pour aller un peu plus loin, on peut imaginer de tronquer le cuboctaèdre pour réaliser le grand rhombicuboctaèdre, mais c'est ici chose impossible à faire directement avec l'option trunc=all] de pst-solides3d, car les faces du cuboctaèdre étant de deux natures différentes (triangles et carrés) on ne peut obtenir les 12 faces carrées régulières, les 8 faces hexagonales régulières et les 6 faces octogonales régulières par ce procédé.
Voici quand même le grand rhombicuboctaèdre à partir des coordonnées prises sur le site :
https://polyhedra.tessera.li/truncated-cuboctahedron/info