Système bielle-manivelle

Le chapitre VII « Généralités sur les courbes » du livre de Henri Bouasse : « Cours de mathématiques générales », paru en 1911 chez Ch.Delagrave à Paris, contient une partie très intéressante intitulée « Déplacement d’une figure invariable », dont j’ai extrait ce court paragraphe (§ 141) ayant pour titre « Système bielle-manivelle », afin de l’illustrer avec PStricks et d’en proposer une animation flash.

« Le point A du plan mobile décrit le cercle de centre O et de rayon OA. Le point B décrit la droite OD que, pour simplifier, nous supposons passer par le centre.
« Le centre instantané de rotation est à l’intersection de la droiteOA(normale au cercle trajectoire du point A) et de la perpendiculaire élevée en B sur la droite OD trajectoire du point B. »
« Nous laissons au lecteur le soin de construire le lieu du centre instantané (indiqué en pointillé sur la figure). Il vérifiera l’existence possible d’une asymptote verticale qui correspond au passage du point A aux extrémités du diamètre EF . Le centre instantané est alors à l’infini : le rotation instantanée devient une translation instantanée ; tous les points de la figure invariable décrivent des arcs parallèles à OD, avec des vitesses égales. »

Pour une animation au format flash :

http://melusine.eu.org/syracuse/mluque/bielle-manivelle/?swf=anim_bielle-manivelle10.swf

Le fichier source PStricks-LaTeX et les animations sont ici :

http://melusine.eu.org/syracuse/mluque/bielle-manivelle/

La loi de Mariotte : une expérience simple

Tous les robinets sont fermés. Le ballon A est rempli de gaz, on a fait le vide dans les 2 autres ballons.

On ouvre le robinet 1, la pression est divisée par 2 :

On ouvre le robinet 2, la pression initiale est divisée par 3 :

Les fichiers :
http://melusine.eu.org/syracuse/G/pstricks/Mariotte/

Le phénomène de l'ébullition

Le phénomène de l'ébullition dessiné avec PStricks et raconté par E.Fernet dans son Précis de Physique, en 1889, un très beau texte.

Le Gif animé a été créé à partir de plusieurs images successives obtenues avec PStricks et un script Perl de Jean-Michel Sarlat. Voici une image obtenue avec PStricks, le code vient tout de suite après le texte.

« Lorsqu’on place de l’eau sur le feu, dans une casserole, on voit apparaître d’abord, quand elle commence à s’échauffer, de petites bulles très fines, qui s’élèvent à la surface. C’est de l’air, qui était en dissolution dans l’eau, et qui se dégage progressivement à mesure que la température s’élève. – Un peu plus tard, on commence à entendre un murmure particulier, qu’on exprime en disant que l’eau chante. En même temps, on aperçoit, au fond du liquide des bulles plus grosses ; mais elles apparaissent et disparaissent subitement, sans monter jusqu’à la surface. Ce sont des bulles de vapeur, qui se forment au contact de la paroi chauffée, mais qui se condensent brusquement, dès qu’elles rencontrent des couches d’eau moins chaudes. C’est le mouvement alternatif, ainsi imprimé à l’eau, qui produit le bruissement dont nous venons de parler. – Enfin, lorsque toute la masse de l’eau est arrivée à la température de 100^o C, de grosses bulles de vapeur s’élèvent dans le liquide, en lui imprimant une agitation tumultueuse, et en venant crever à sa surface. C’est le phénomène de l’ébullition. »

Précis de Physique, E.FERNET 1889.

\documentclass[12pt]{article}
\usepackage[a4paper]{geometry}
\usepackage[garamond]{mathdesign}
\renewcommand{\ttdefault}{lmtt}
\usepackage[frenchb]{babel}
\usepackage{pst-grad,multido}%
\input{random.tex}         % From Donald Arseneau (on macros/generic on CTAN)
% Manuel Luque
%  6 avril 2003
% révision du 28 octobre 2011
\SpecialCoor
\definecolor{Bluea}{cmyk}{.2,0,0,0}
\definecolor{BleuVerre}{cmyk}{.2,0,0,0.4}
\definecolor{OrangePale}{cmyk}{0,0.2,0.4,0}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\makeatletter
\def\casserole{%
 \psclip{%
    \pscustom[linestyle=none]{%
        \psline(-2,2.5)(-2,0)
        \psellipticarc(0,0)(2,0.2){180}{0}
        \psline(2,0)(2,2.5)}}
    \psclip{\pscustom[linecolor=cyan,fillstyle=solid,fillcolor=Bluea]{%
      \psellipticarc(0,1.5)(2,0.2){0}{180}
      \psline(-2,1.5)(-2,0)
      \psellipticarc(0,0)(2,0.2){180}{0}
      \psline(2,0)(2,1.5)}}
            \BILLES
      \endpsclip
 \endpsclip
 \psellipse[linecolor=blue,fillstyle=vlines,hatchcolor=blue,hatchsep=0.2\pslinewidth,hatchwidth=0.5\pslinewidth](0,1.5)(2,0.2)
 \bgroup
 \psset{linecolor=BleuVerre}
 \psline(-2,0)(-2,2.5)
 \psellipticarc(0,0)(2,0.2){180}{0}
 \pscustom[linewidth=2\pslinewidth]{%
 \psline[linearc=0.1](-0.2,2.3)(0,2.1)(0.2,2.3)
    \psellipticarc(0,2.5)(2.1,0.2){-38}{218}
    \closepath
    }
 \pscustom{%
    \psarcn(2.5,1.7){0.5}{180}{90}
    \psline(2.5,2.2)(7,2.2)
    \psarc(7,2.35){0.15}{-90}{90}
    \psline(7,2.5)(2,2.5)
    \psline(2,2.5)(2,1.7)
    \fill[fillstyle=solid,fillcolor=BleuVerre]}
 \psline(2,0)(2,2.5)
 \egroup}
% idée empruntée à Denis Girou dans pst-labo
\newdimen\BX
\newdimen\BY
\newdimen\RAYONBULLE
\makeatletter
\newcommand{\BILLES}[1][50]{%
\multido{\IBULLE=1+1}{#1}{%
\setrandim{\BX}{-2\psunit}{2\psunit}
\setrandim{\BY}{0\psunit}{2\psunit}
\pst@dimh=\BY
\setrandim{\RAYONBULLE}{0.01\psunit}{0.15\psunit}
\ifdim\BY>2\psunit \multiply \RAYONBULLE by 3
\else
    \ifdim\BY < 2\psunit \ifdim\BY >1\psunit \multiply \RAYONBULLE by 2\fi
    \else
     \multiply \RAYONBULLE by 1
    \fi
\fi
\rput(0,0){%
\pscircle[style=BilleThreeD](\BX,\BY){\RAYONBULLE}}}}
%
\newpsstyle{BilleThreeD}{linestyle=none,fillstyle=gradient,gradmidpoint=0,gradend=white}
%
\def\BecBunsenGrille{%
\psframe(-1.25,0)(1.25,0.25)
\psframe(-.5,1.25)(0.5,2.25)
\multido{\n=-0.3+0.3}{3}{%
\pscircle(\n,1.75){0.1}}
\psframe(-.25,2.25)(0.25,4.25)
\psline(0.25,1.25)(0.25,0.5)(1.25,0.25)
\psline(-1.25,0.25)(-.25,0.5)(-0.25,0.75)
\psline(-2.25,0.75)(-.25,0.75)
\psline(-2.25,1)(-.25,1)
\psellipse(-.25,0.875)(0.1,0.125)
\psframe[fillstyle=solid,linestyle=none](-2.25,0.75)(-0.25,1)
\psline(-2.25,0.75)(-0.25,0.75)
\psline(-2.25,1)(-0.25,1)(-.25,1.25)
\pscurve(-0.25,0.5)(0,0.4)(0.25,0.5)
%flamme
\rput(0,4.25){%
\psclip{\pstFlammeGrille}%
\pspolygon[linestyle=none,fillstyle=gradient,gradmidpoint=0,gradbegin=cyan,gradend=white]%
(-0.25,0)(0.25,0)(0,1)%
\endpsclip}
\psline[linestyle=dashed,linewidth=0.08](-2,5.75)(2,5.75)}
%
\def\pstFlammeGrille{%
\pscustom[linestyle=none]{%
\psarc(0,0.75){0.75}{270}{0}
\psarcn(1.5,0.75){0.75}{180}{90}
\psline(1.5,1.5)(-1.5,1.5)
\psarcn(-1.5,0.75){0.75}{90}{0}
\psarc(0,0.75){0.75}{180}{270}
\fill[style=flammeEtGrille]}}
%
\newpsstyle{flammeEtGrille}{linestyle=none,fillstyle=gradient,%
gradmidpoint=0,gradbegin=OrangePale,gradend=yellow}
\makeatother
\pagestyle{empty}
\begin{document}
\begin{center}
\begin{pspicture}(-3,-6)(3,5)
\casserole
\rput(0,-6){\BecBunsenGrille}
\end{pspicture}
\end{center}
<< Lorsqu'on place de l'eau sur le feu, dans une casserole, on voit
apparaître d'abord, quand elle commence à s'échauffer, de petites bulles très fines, qui s'élèvent à la surface.
C'est \textit{de l'air}, qui était en dissolution dans l'eau, et qui se dégage
progressivement à mesure que la température s'élève. -- Un peu plus tard, on
commence à entendre un murmure particulier, qu'on exprime en disant que
\textit{l'eau chante}. En même temps, on aperçoit, au fond du liquide des
bulles plus grosses ; mais elles apparaissent et disparaissent subitement,
sans monter jusqu'à la surface. Ce sont des bulles de vapeur, qui se
forment au contact de la paroi chauffée, mais qui se condensent brusquement,
dès qu'elles rencontrent des couches d'eau moins chaudes. C'est le mouvement
alternatif, ainsi imprimé à l'eau, qui produit le bruissement dont nous
venons de parler. -- Enfin, lorsque toute la masse de l'eau est arrivée à la
température de $100^{\mathrm{o}}$~C, de grosses bulles de vapeur s'élèvent
dans le liquide, en lui imprimant une agitation tumultueuse, et en venant crever à sa surface. C'est le
phénomène de \textit{l'ébullition}. >>
\begin{flushright}
Précis de Physique, E.\textsc{Fernet} 1889.
\end{flushright}
\end{document}
 

Un peu de géométrie avec PStricks

Un exemple de figure géométrique réalisée avec PStricks.

Le code :
\documentclass{article}
\usepackage{pst-node}
\usepackage{pst-plot}
\usepackage[T1]{fontenc}
\usepackage[latin1]{inputenc}
\SpecialCoor
\newcommand{\Radius}{5}
\newcommand{\Xc}{5}
\psset{dimen=middle}
\pagestyle{empty}
\title{Un peu de géométrie avec PStricks \\ exemple 1}
\author{http://melusine.eu.org/syracuse/G/pstricks/}
\date{2 avril 2002--28 octobre 2011}
\begin{document}
\maketitle
\begin{center}
\begin{pspicture}(-\Radius,-\Radius)(\Radius,\Radius)
\pscircle{\Radius}
\psframe(-\Radius,-\Radius)(\Radius,\Radius)
\newcommand\MotifCoin{%
\pnode(!
    /Xc \Xc\space def
    /Radius \Radius\space def
    /radius1 Xc 2 Radius mul add Xc Radius mul Radius dup mul add
    sqrt 2 mul sub def
    /X1 radius1 def
    X1 radius1){PointInitial}
\parametricplot{0}{360}{%
    t cos radius1 mul radius1 add Radius sub
    t sin radius1 mul radius1 add Radius sub}
\multido{\i=0+1}{30}{%
\pnode(!
    /B Radius X1 mul Xc radius1 mul sub neg def
    /A Radius radius1 sub def
    /C X1 X1 mul Radius mul Xc Xc mul radius1 mul sub def
    /Discriminant B B mul A C mul sub sqrt def
    /X2 B neg Discriminant add A div def
    /radius2 X2 X1 sub 2 exp 4 radius1 mul div def
    X2 radius2){PointIntermediaire}
%Sur Ox
\parametricplot{0}{360}{%
    t cos radius2 mul X2 add Radius sub
    t sin radius2 mul radius2 add Radius sub
    }
%Sur Oy
\parametricplot{0}{360}{%
    t sin radius2 mul radius2 add Radius sub
    t cos radius2 mul X2 add Radius sub
    }
\pnode(!
    /X1 X2 def
    /radius1 radius2 def
    X1 radius1){fictif2}
    }}
\multido{\i=0+90}{4}{%
\rput{\i}{\MotifCoin}}
\end{pspicture}
\end{center}
\end{verbatim}
\end{document}

Position des planètes, celles qui sont visibles à l’œil nu, en projection sur le plan de l'écliptique

Ce package pst-solarsysteme permet de représenter toutes les planètes en projection sur le plan de l'écliptique à une date choisie. Seules Mercure, Vénus, Terre et Mars voient les proportions des orbites et de leurs tailles relatives respectées. Saturne et Jupiter sont dans la bonne direction, mais évidemment pas à la bonne distance.

Les orbites sont représentées en trait continu pour la partie au-dessus de l'écliptique et en pointillés pour la partie située en-dessous.

Une option \[values=true] est activée par défaut. Elle permet d'afficher les valeurs de la longitude, de la latitude et de la distance en unité astronomique, ce qui permettra de les comparer aux éphémérides du bureau des longitudes.

Ce package, élaboré sous Git est disponible à l'adresse suivante :

http://melusine.eu.org/syracuse/G/pstricks/planetes/

pst-anamorphosis

Tous les types d'anamorphoses : cylindrique, conique, sphérique et perspective ont été repris de A à Z par l'équipe suivante : Jürgen Gilg, Manuel Luque et Jean-Michel Sarlat.
Désormais il n'existe plus qu'un seul package : pst-anamorphosis.
Voici quelques-unes des nouvelles possibilités parmi les plus intéressantes :

1) anamorphose directe d'une image au format eps ;
2) mise au point d'un script "psftopst.pl" permettant de transformer un fichier au format Flattened PostScript 1 en un fichier embarquant les commandes équivalentes pour PSTricks, ce fichier a le suffixe .pst.
Dans le cadre des anamorphoses, les fichiers PST présentent l’intérêt d’être directement incorporés dans le fichier qui sera, au final, transformé en PDF.
3) Mise au point d'un d'un script "epsnorm.pl" dont le but est de normaliser une image au format eps pour permettre soit son anamorphose directe soit sa transformation en fichier au format .pst.

Désormais tout ce qui concerne ce package est à l'adresse suivante :

http://melusine.eu.org/syracuse/G/pst-anamorphosis/

Ce package fait partie des "projets Syracuse sous Git". Vous trouverez à cette adresse :

http://melusine.eu.org/syracuse/G/

tous les détails pour participer à l'un des projets si vous le souhaitez.

Perspective à rebours

 Il y a maintenant un booléen perpsective=true qui représente l'objet traité en perspective et qui positionné à false donne la représentation inversée c'est-à-dire l'anamorphose oblique.
Ceci est extrait de la page 59 du Baltrušaïtis.
« L'arrangement peut fonctionner dans les deux sens. Si le carré en perspective se présente comme un trapèze, le trapèze y apparaît comme un carré.
Un renversement du point de vue ramené au dessus du point principal (à une hauteur égale à l'éloignement de la distance) et installé en quelque sorte dans le tableau, aboutit à un effet contraire. Les mêmes rétrécissements corrigent les formes et les rapprochent au lieu de les éloigner et de les altérer, comme dans un film à l'envers. La perspective est à rebours. »

 Les fichiers :
http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/anamorphose_oblique

L'anamorphose oblique ou perspective

Dans le livre de Jurgis Baltrušaïtis Anamorphoses : les perspectives dépravées en livre de poche chez Flammarion.}, on trouve le principe de la « costruzione legittima » avec un schéma de Léonard de Vinci (1492) et des schémas anamorphiques de Niceron (1658). Je cite page 58 :

« Rappelons en quelques mots quels ont été le procédés utilisés par les artistes pour l'ordonnancement de leurs tableaux en perspective normale. La première ligne tracée est celle de l'horizon à la hauteur de l’œil. Deux points y sont ensuite fixés : au milieu le point principal vers où convergent toutes les lignes droites parallèles qui s'éloignent en profondeur ; sur la même horizontale et à la même distance du point principal que l’œil, en face de la composition -- le point de distance, vers lequel convergent les diagonales.»
Voici quelques illustrations réalisées avec PStricks :

 

Les fichiers :

http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/anamorphose_oblique

La tour Eiffel par l'anamorphose conique.

Voici la tour Eiffel, convertie en commandes PStricks par Jean-Michel Sarlat, subissant l'anamorphose conique.

Les fichiers :
http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/anamorphose_conique

Anamorphose pyramidale

La pyramide est le miroir ou plutôt ce sont les quatre faces qui sont les miroirs, l'observateur se place au-dessus de la pyramide.
Dans le cas général il suffit de découper le contour et de rabattre les triangles latéraux pour obtenir la « bonne » pyramide.
L'image anamorphosée est une « Étude de mouvement : basse-cour » de Vasarely datée de 1939.
Au centre l'image restituée, qui est l'image initiale et qui sera vue en se plaçant au-dessus de la pyramide.
L'image anamorphique est constituée des quatre triangles latéraux.

Les fichiers :
http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/anamorphose_pyramidale

Quelques macros de pst-optic utiles pour construire rayons et faisceaux incidents et réfléchis par un miroir plan

En préambule à l'anamorphose dans un miroir plan, quelques macros de pst-optic utiles pour construire rayons et faisceaux incidents et réfléchis par un miroir plan.
\planMirrorRay(A)(M1)(M2){A'}
A est la source (le point objet), M1 et M2 les deux extrémités du miroir et A' est le point image obtenu.

 \symPlan(M1)(M2){objet}
L'objet est décrit par des commandes PSricks ou bien ce peut être une image eps avec \includegraphics{image.eps}

\begin{pspicture}(-5,-5)(5,8)
\rput(-2,2){\BecBunsen}
\pnode(-5,-3){M1}
\pnode(5,5){M2}
\uput[-90](M1){M1}
\uput[90](M2){M2}
\psline[linewidth=5\pslinewidth](M1)(M2)
\ncline[linewidth=4\pslinewidth,linecolor=BleuVerre]{M1}{M2}
\psset{linestyle=dashed}
\symPlan(M1)(M2){\rput(-2,2){\BecBunsen}}
\end{pspicture}

Les fichiers :
http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/anamorphose_pyramidale

Voir dans un miroir : une autre anamorphose

 

Il s'agit d'un miroir plan incliné d'un angle $\alpha$ par rapport

à l'horizontale. L'image anamorphosée est posée sur la table
horizontale devant le miroir et l'observateur se place au-dessus
du miroir pour regarder l'image dans le miroir.

Le repère choisi $(Oxyz)$ est tel que $(Oxz)$ est le plan vertical et
$(Oxy)$ le plan horizontal avec $(Oy)$ dirigé vers l'arrière de la
feuille.

Appelons $(\Delta)$ la droite représentant le plan du miroir dans le
plan $(Oxz)$, son équation s'écrit :
$$z=-(\tan\alpha)x$$
$A'(x'_A,z'_A)$ symétrique de $A(x_A,0)$ par rapport à $(\Delta)$ remplit la double
condition :
            1) $(AA')$ et $(\Delta)$ sont perpendiculaire

            2)

           3) Le milieu H de (AA') appartient au plan du miroir.

En portant z_A' dans la première condition :

 Après réarrangement et simplifications, on obtient :

Mais comme il s'agit de construire l'image anamorphosée, celle que l'on va placer devant le miroir et dont le miroir rendra la forme exacte, ce sont les formules inverses qu'il faut appliquer ( z_A' n'a pas d'utilité ici) :

 Si l'on considère une image que l'on souhaite anamorphoser (afin de la reconstituer dans le miroir), cette image étant située dans le plan Oxy, il faudra donc appliquer les transformations suivantes à chaque point A'( x_A' , y_A' ) de cette image :

 

\documentclass[12pt]{article}
\usepackage[T1]{fontenc}
\usepackage{pst-node}
\usepackage{pst-3d}
\usepackage{pst-grad}
\usepackage{multido}
\usepackage{pst-eucl}
\usepackage{pst-slpe}
\usepackage{enumerate}
\usepackage{amsmath}
\usepackage[a4paper,width=17cm]{geometry}
\definecolor{OrangePale}{cmyk}{0,0.2,0.4,0}
\SpecialCoor
\psset{dimen=middle}
\makeatletter
\define@key[psset]{}{inclinaison}{\edef\psk@inclinaison{#1}}
\psset{inclinaison=60}
%
\def\VoirDansUnMiroir{\@ifnextchar[{\pst@VoirDansUnMiroir}{\pst@VoirDansUnMiroir[]}}
\def\pst@VoirDansUnMiroir[#1]{\pst@killglue\pst@makebox{\VoirDansUnMiroir@[#1]}}
\def\VoirDansUnMiroir@[#1]{{%
\psset{#1}%
\leavevmode
\hbox{%
\pnode(!%
/Inclinaison \psk@inclinaison\space def
/ax 1 2 Inclinaison mul cos div def
/by 0 def
/cx 0 def
/dy 1 def
cx dy){Factice}%
\pst@Verb{%
{ [ax by cx dy 0 0] concat
} \tx@TMChange}%
\box\pst@hbox
\pst@Verb{\tx@TMRestore}}%
}}
\makeatother
\def\poisson{%
\begingroup
\psset{fillstyle=slope}
\pscurve(0.1,1.8)(0.4,1.65)(0.6,1.1)(0.85,1.2)
\pscurve(1.6,3.25)(2.5,4.2)(2.5,3.5)
\pscurve(4.25,1.9)(4.5,1.5)(3.9,1.4)(3.7,0.8)(3.2,1.5)
\pscurve(2.5,3.5)(2.75,3.75)(3.2,4)(3.75,3.2)(3.2,2.8)%(2.8,3.2)
\pscurve(5,2.45)(6,2.5)(5.75,2)(6,1.5)(5.8,1.4)(5,1.6)
\pscurve(3.2,1.4)(3.1,0.7)(3.5,0.5)(2.7,0.5)
\pscurve(1.8,1.1)(2.2,1.4)(2.7,1.6)(2.6,1.2)(2.65,1.1)
(2.6,1)(2.65,0.9)(1.9,0.5)
\endgroup
\pscurve[fillstyle=slopes](0.25,2.4)(1,3)(1.6,3.25)(2.5,3.5)(3,3)(4,2.6)
(5,2.45)(5.7,2.75)(6,2.5)(5.75,2)(6,1.5)(5.9,1.35)(5,1.6)
(4,1.7)(3,1.1)(2.7,-.2)(2,0)(1,0.3)(0.8,0.3)(0.35,1)
(0.1,1.8)(0,2.1)(0.1,2.2)(0.5,1.9)(0.45,2.2)(0.25,2.4)
\pscircle(0.9,2.5){0.25}
\pscircle*(0.9,2.5){0.15}
\pscircle[fillstyle=solid,linestyle=none](0.85,2.55){0.03}
\pscurve(0.35,1)(1,0.8)(1.45,1)(1.6,1.6)(1.5,2.25)}
\definecolor{BleuVerre}{cmyk}{0.2,0,0,0}
%
\def\oeil{\psarc[linewidth=2pt](0,2.5){2.5}{215}{270}%
\psarc[linewidth=2pt](0,-2.5){2.5}{90}{140}%
\psarc(-2.5,0){1}{-30}{30}%
\psarc(0,0){1.75}{160}{200}
\psclip{%
\pscircle[linestyle=none](0,0){1.75}}
\pscircle[fillstyle=solid,fillcolor=lightgray](-2.5,0){0.9}
\endpsclip}%
%definition de Dominique Rodriguez in Euclide.tex
\newcommand{\Vecteur}[1]{\ensuremath{\overrightarrow{#1\hspace{.3em}}}}%
%
\title{Anamorphose dans un miroir plan}
\date{23 juillet 2001\\révision 5 octobre 2011}
\author{Team ``http://melusine.eu.org/syracuse/G/pstricks/''}
\begin{document}
\maketitle
\newcommand\Poisson{\rput(-6,0){\poisson}}
\begin{center}
\begin{pspicture}(-6,0)(11,4)
\psgrid[gridcolor=lightgray](-6,4)%
\Poisson
\VoirDansUnMiroir[inclinaison=60]{\psgrid(-6,4)\Poisson}
\end{pspicture}
\begin{verbatim}
\VoirDansUnMiroir[inclinaison=60]{\psgrid(-6,4)\Poisson}
\end{verbatim}
\end{center}
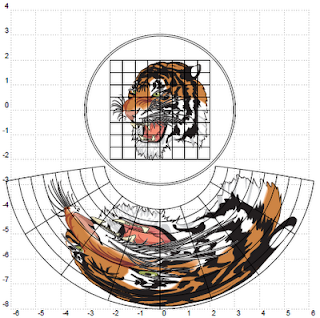
L'image anamorphosée est à droite. La feuille étant posée horizontalement, une arête du miroir se place sur le ligne commune et le miroir doit être incliné de 60$^\circ$ (ou de l'angle pour lequel l'image a été calculée) avec l'horizontale vers la gauche. On regarde au-dessus, l'image observée dans le miroir doit être identique à l'image située à gauche sur le dessin.
\begin{center}
\begin{pspicture}(-3.5,-3)(12.5,4)
\psgrid[gridcolor=lightgray](-4,-3)(0,3)%
\rput(-2.2,0){\psset{unit=0.5}\input{parrot.tex}}
\VoirDansUnMiroir[inclinaison=54]{\psgrid[gridwidth=0.5\pslinewidth](-4,-3)(0,3)\rput(-2.2,0){\psset{unit=0.5}\input{parrot.tex}}}
\end{pspicture}
\begin{verbatim}
\VoirDansUnMiroir[inclinaison=54]{input{parrot.tex}}
\end{verbatim}
\end{center}
\end{document}
Le fichier du perroquet :
http://melusine.eu.org/syracuse/W/download/syracuse/G/pstricks/Anamorphoses/parrot.tex

Anamorphose conique

Une étude théorique de l'anamorphose conique, des macros PStricks pour expérimenter, une documentation et quelques exemples.

Les fichiers :
http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/anamorphose_conique/
ou
http://manuel.luque.perso.neuf.fr/Anamorphoses/anamorphose_conique/

Anamorphose sphérique (suite)

Le code se précise. La documentation est un pu plus détaillée et les exemples plus nombreux.

http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/anamorphose_spherique/

Anamorphose cylindrique : partie 4

Grâce à Jean-Michel Sarlat qui peaufine son script permettant de coder un fichier .eps  en macros PStricks, la bibliothèque d'images s'enrichit :

Les fichiers :

pst-anamorphosis

ou

https://melusine.eu.org/syracuse/G/pst-anamorphosis/ 

Anamorphose cylindrique : le perroquet

Toujours grâce au script de Jean-Michel, voici l'anamorphose du perroquet.

 

Les fichiers : ACparrot.tex, parrot.tex, exemple_parrot.tex  et exemple_parrot.pdf sont dans le répertoire :

 pst-anamorphosis

le fichier  pst-anamorphosis.zip de ce répertoire contient tous les fichiers.

ou

http://melusine.eu.org/syracuse/G/pstricks/Anamorphoses/