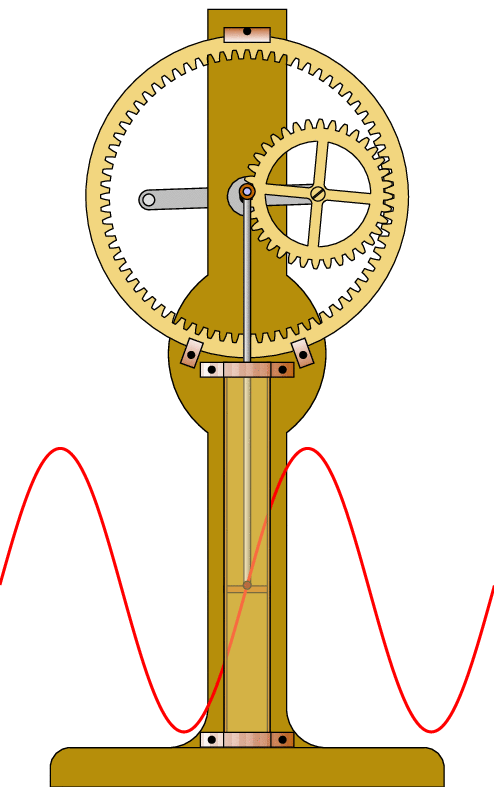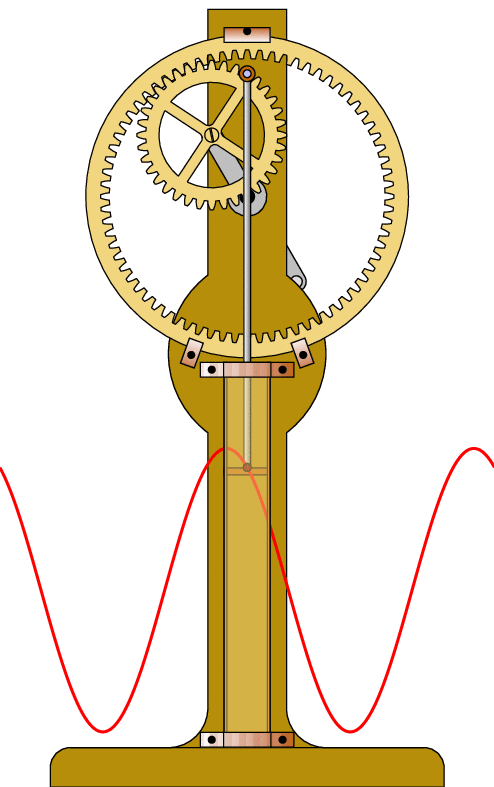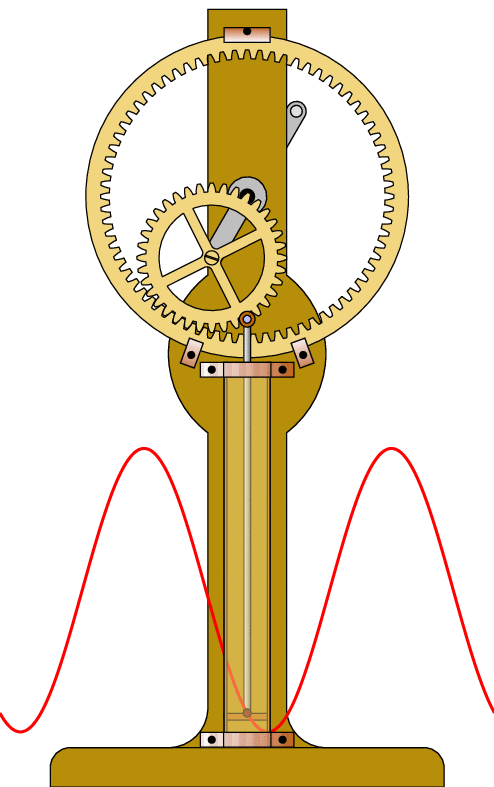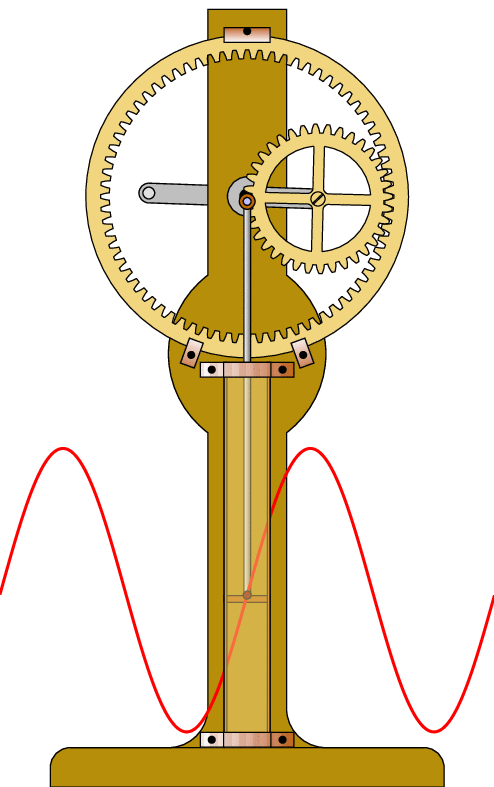
Les schémas :
C'est un exercice que j'ai trouvé dans deux manuels de physique :
"Lagrangian Dynamics" de Dare A.Wells (Schaum's Outline Series in Engineering 1967) pages 12-13 (Figure 2.8) et sous le titre "Système de deux masselottes en interaction élastique et en chute libre" exercice E25-1 dans le livre ``Leçons de physique'' de José-Philippe Pérez, Pujol, Lacoute et Desmeule édité par De Boeck en 2011, ce dernier propose une solution mais ne tient pas compte des rayons respectifs des billes.
Le ressort de longueur initiale (à vide) $l_0$ est sans masse et a pour raideur $k$, les deux billes ont pour masses et rayons respectifs $m_1$, $r_1$ et et $m_2$, $r_2$.
À l'origine des dates $t=0$ le système est en équilibre, le ressort est étiré par le poids de la bille 2.
\[
m_2g=k\Big(\big(z_2(0)-z_1(0)\big)-(r_1+r_2)-l_0\Big)
\]
$z_1(0)=0$ du fait du choix de l'origine de l'axe, on en déduit $z_2(0)$ :
\[
z_2(0)=(r_1+r_2)+l_0+\frac{m_2g}{k}
\]
et la position du centre de masse du système :
\[
z_G(0)=\frac{m_2}{m_1+m_2}\Big((r_1+r_2)+l_0+\frac{m_2g}{k}\Big)
\]
À un instant $t$ quelconque, la longueur du ressort vaut :
\[
l(t)=z_2(t)-z_1(t)-(r_1+r_2)
\]
et son allongement(ou compression) :
\[
\Delta l(t)=l(t)-l_0
\]
La relation fondamentale de la dynamique appliquée à chacune des deux billes donne :
\[
m_1\ddot{z_1}=\hphantom{-}k\big((z_2-z_1)-(r_1+r_2)-l_0\big) + m_1g
\]
\[
m_2\ddot{z_2}=-k\big((z_2-z_1)-(r_1+r_2)-l_0\big) + m_2g
\]
\begin{equation}
\ddot{z_1}=\hphantom{-}\frac{k}{m_1}\big((z_2-z_1)-(r_1+r_2)-l_0\big) + g
\end{equation}
\begin{equation}
\ddot{z_2}=-\frac{k}{m_2}\big((z_2-z_1)-(r_1+r_2)-l_0\big) + g
\end{equation}
on choisit comme variable $Z=z_2-z_1$, $\ddot{Z}=\ddot{z_2}-\ddot{z_1}$.
\[
\ddot{Z}=-k\Big(Z-(r_1+r_2)-l_0\Big)\Big(\frac{1}{m_1}+\frac{1}{m_2}\Big)
\]
En posant $\mu=\dfrac{m_1m_2}{m_1+m_2}$, l'équation différentielle en $Z$ s'écrit :
\[
\ddot{Z}+\frac{k}{\mu}Z=\frac{k}{\mu}\big((r_1+r_2)+l_0\big)
\]
$\omega_0^2=\dfrac{k}{\mu}$
\[
\ddot{Z}+\omega_0^2Z=\omega_0^2(r_1+r_2+l_0)
\]
Compte-tenu des conditions initiales : $Z(0)=z_2(0)$ et $\dot{Z}(0)=0$, la solution de cette équation est :
\[
Z(t)=\frac{m_2g}{k}\cos\omega_0t+r_1+r_2+l_0
\]
On peut en déduire $z_1(t)$ et $z_2(t)$, sachant que :
\[
z_G(t)=\frac{m_1z_1(t)+m_2z_2(t)}{m_1+m_2}
\]
d'où
\[
z_1(t)=z_G(t)-\frac{m_2}{m_1+m_2}Z(t)
\]
Et que :
\[
z_G(t)=\frac{1}{2}gt^2+z_G(0)
\]
\[
z_2(t)=z_1(t)+Z(t)=z_G(t)+\frac{m_1}{m_1+m_2}Z(t)
\]
Le package "pst-massspring" ne comprend qu'une seule commande \psMS[options], dont les options et leurs valeurs par défaut sont les suivantes :
- t=0 : le temps en secondes ;
- m1=0.5 : masse de (1) en kg ;
- m2=2 : masse de (2) en kg ;
- k=7.5 : constante de raideur N/m ;
- l0=5 : longueur initiale du ressort.
Les rayons sont calculés à partir des masses (on suppose que toutes deux sont en acier). Ce package a été écrit pour créer des animations, en voici deux, la première avec les valeurs par défaut.
La deuxième avec m1=m2=1 et k=10
Les fichiers sont compris dans l'archive .zip qui comprend aussi les packages pst-massspring et pst-ressort(ce dernier contient de nombreux autres exemples sur ce site).
Chute-libre-de-deux-masses-reliees-par-un-ressort.zip
ou sur drive
Chute-libre-de-deux-masses-reliees-par-un-ressort.zip
La compilation des fichiers s'effectue avec la procédure classique pour PSTricks, par exemple :
LaTeX pst-massspring-anim1.tex
dvips pst-massspring-anim1.dvi
ps2pdf pst-massspring-anim1.ps
convert -delay 5 -density 100x100 -alpha remove pst-massspring-anim1.pdf[1-1000] -loop 0 pst-massspring-anim1.gif