jeudi 28 avril 2016
Illustration de la loi de Mariotte (Boyle) - 2
\documentclass{article}
\usepackage[a4paper]{geometry}
\usepackage[garamond]{mathdesign}
\usepackage{pstricks,multido}%
\input{random} % From Donald Arseneau (on macros/generic on CTAN)
\pagestyle{empty}
\psset{dimen=middle}
\newdimen{\BulleX}
\newdimen{\BulleY}
\newdimen\X
\newdimen\Y
\newdimen\Coor
% Random walk in the unit square (#1 = number of steps)
% idée empruntée à Denis Girou
\def\RandomMolecule#1{%
\multido{\i=1+1}{#1}{%
\setrandim\X{-2pt}{2pt}
\setrandim\Y{-2pt}{2pt}
\pscircle*[linecolor=blue](\pointless\X,\pointless\Y){0.03} % Initial point
}}
%
\newcommand\ballon{%
\pscustom{\psline(-0.75,2.75)(-0.5,2.5)(!-0.5 19.5 cos 1.5 mul)
\psarc(0,0){1.5}{110}{70}
\psline(!0.5 19.5 cos 1.5 mul)(0.5,2.5)(0.75,2.75)}}
\newcommand\ballonA{%
\pscustom{\psline(-0.5,2.5)(!-0.5 19.5 cos 1.5 mul)
\psarc(0,0){1.5}{110}{70}
\psline(!0.5 19.5 cos 1.5 mul)(0.5,2.5)}}
\newcommand\bouchon{%
\pspolygon[fillstyle=solid,fillcolor=lightgray]%
(-0.53,0.5)(-0.45,-0.5)(0.45,-0.5)(0.53,0.5)}
\newcommand\tubeA{%
\psline[doubleline=true,doublesep=0.15,linearc=0.25](-2.3,-2.8)(-2.3,0)(2.3,0)(2.3,-2.8)
}
\newcommand\tubeC{%
\psline[doubleline=true,doublesep=0.15,linearc=0.25](2.3,-2.8)(2.3,0)(0,0)
}
\newcommand\tubeD{%
\psline[doubleline=true,doublesep=0.15,linearc=0.25](-2.3,-2.8)(-2.3,0)(0,0)
}
\newcommand\tubeB{%
\psline[doubleline=true,doublesep=0.15,linearc=0.25](0,-2.8)(0,0)(-3,0)}
\newcommand\manometre[2]{%
\rput(0.2,0){%
\psline[doubleline=true,doublesep=0.15,doublecolor=cyan!#2](0,0)(0,-5)
\pscircle[doubleline=true,fillstyle=solid](0,0){1}
\psarc(0,0){0.65}{-60}{240}
\multido{\i=-60+30}{11}{\psline(0.65;\i)(0.45;\i)}
\psline[linewidth=0.05]{->}(!0.5 #1 cos mul 0.5 #1 sin mul)%
(!0.5 #1 180 add cos mul 0.5 #1 180 add sin mul)
\pscircle[fillstyle=solid]{0.1}}}
\newcommand\robinetouvert{
\pspolygon[fillstyle=solid,fillcolor=lightgray,linearc=0.02](-0.3,0.35)(0.3,0.35)(0.3,0.2)(0.1,0.2)
(0.1,0.07)(-0.1,0.07)(-0.1,0.2)(-0.3,0.2)(-0.3,0.3)
\pspolygon[fillstyle=solid,fillcolor=lightgray,linearc=0.02](-0.1,-0.07)(-0.1,-0.35)(0.1,-0.35)(0.1,-0.07)
}
\newcommand\robinetferme{
\pspolygon[fillstyle=solid,fillcolor=lightgray,linearc=0.02](-0.05,0.3)(-0.05,-0.35)(0.05,-0.35)(0.05,0.3)
\pscircle[fillstyle=solid,fillcolor=lightgray](0,0.25){0.1}}
\pagestyle{empty}
\title{Illustration de la loi de Mariotte}
\date{29 octobre 2011}
% http://pstricks.blogspot.fr/2011/10/la-loi-de-mariotte-une-experience.html
\begin{document}
\psset{unit=0.5}
\noindent Tous les robinets sont fermés. Le ballon A est rempli de gaz, on a fait le vide dans les 2 autres ballons.
\begin{center}
\begin{pspicture}(-8,-2)(6,7)%\psgrid
% On place d'abord le ballon qui contient le gaz initial
\rput(4,0){\psset{fillstyle=solid,fillcolor=cyan!30}
\psclip{\ballonA}
\RandomMolecule{600}
\endpsclip}
% On place d'abord les tubes
\multido{\N=-3.5+5.0}{2}{\rput(\N,3.8){\tubeA}}
\rput(1.5,3.8){\psset{doublecolor=cyan!30}\tubeC}
\rput(-6.2,3.8){\tubeB}
% on place les robinets
\uput[u](1.5,4.2){R1}
\uput[u](-3.5,4.2){R2}
\uput[u](-8,4.2){R3}
\rput(1.5,3.8){\robinetferme}
\rput(-8,3.8){\robinetferme}
\rput(-3.5,3.8){\robinetferme}
% On place le manomètre
\rput(4,6){\manometre{-30}{30}}
% On redessine ensuite les trois ballons avec leurs bouchons
\multido{\i=-6+5}{3}{\rput(\i,0){\ballon}\rput(\i,2.25){\bouchon}}
\rput(4,0){A}\rput(-1,0){B}\rput(-6,0){C}
\uput[r](5.25,6){$\mathrm{P_0}$}
\end{pspicture}
\end{center}
On ouvre le robinet 1, la pression est divisée par 2 :
\begin{center}
\begin{pspicture}(-8,-2)(6,7)%\psgrid
% On place d'abord le ballon qui contient le gaz initial
\rput(4,0){\psset{fillstyle=solid,fillcolor=cyan!20}
\psclip{\ballonA}
\RandomMolecule{300}
\endpsclip}
\rput(-1,0){\psset{fillstyle=solid,fillcolor=cyan!20}
\psclip{\ballonA}
\RandomMolecule{300}
\endpsclip}
% On place d'abord les tubes
\rput(1.5,3.8){\psset{doublecolor=cyan!20}\tubeA}
\rput(-3.5,3.8){\tubeA\psset{doublecolor=cyan!20}\tubeC}
\rput(-6.2,3.8){\tubeB}
% on place les robinets
\uput[u](1.5,4.2){R1}
\uput[u](-3.5,4.2){R2}
\uput[u](-8,4.2){R3}
\rput(1.5,3.8){\robinetouvert}
\rput(-8,3.8){\robinetferme}
\rput(-3.5,3.8){\robinetferme}
% On place le manomètre
\rput(4,6){\manometre{-135}{20}}
% On redessine ensuite les trois ballons avec leurs bouchons
\multido{\i=-6+5}{3}{\rput(\i,0){\ballon}\rput(\i,2.25){\bouchon}}
\rput(4,0){A}\rput(-1,0){B}\rput(-6,0){C}
\uput[r](5.25,6){$\mathrm{P_1=\displaystyle\frac{P_0}{2}}$}
\end{pspicture}
\end{center}
On ouvre le robinet 2, la pression initiale est divisée par 3 :
\begin{center}
\begin{pspicture}(-8,-2)(6,7)%\psgrid
% On place d'abord le ballon qui contient le gaz initial
\rput(4,0){\psset{fillstyle=solid,fillcolor=cyan!10}
\psclip{\ballonA}
\RandomMolecule{200}
\endpsclip}
\rput(-6,0){\psset{fillstyle=solid,fillcolor=cyan!10}
\psclip{\ballonA}
\RandomMolecule{200}
\endpsclip}
\rput(-1,0){\psset{fillstyle=solid,fillcolor=cyan!10}
\psclip{\ballonA}
\RandomMolecule{200}
\endpsclip}
% On place d'abord les tubes
\rput(1.5,3.8){\psset{doublecolor=cyan!10}\tubeA}
\rput(-3.5,3.8){\psset{doublecolor=cyan!10}\tubeA}
\rput(-8.5,3.8){\psset{doublecolor=cyan!10}\tubeC}
% on ajuste l'extrémité du tube de sortie
\psline[doubleline=true,doublesep=0.15](-8.05,3.8)(-9.2,3.8)
% on place les robinets
\uput[u](1.5,4.2){R1}
\uput[u](-3.5,4.2){R2}
\uput[u](-8,4.2){R3}
\rput(1.5,3.8){\robinetouvert}
\rput(-8,3.8){\robinetferme}
\rput(-3.5,3.8){\robinetouvert}
% On place le manomètre
\rput(4,6){\manometre{-190}{10}}
% On redessine ensuite les trois ballons avec leurs bouchons
\multido{\i=-6+5}{3}{\rput(\i,0){\ballon}\rput(\i,2.25){\bouchon}}
\rput(4,0){A}\rput(-1,0){B}\rput(-6,0){C}
\uput[r](5.25,6){$\mathrm{P_2=\displaystyle\frac{P_0}{3}}$}
\end{pspicture}
\end{center}
\end{document}
Ébullition et pression (trompe à eau~water pump)
\documentclass{article}
\usepackage{pst-grad,multido}%
\input{random.tex} % From Donald Arseneau (on macros/generic on CTAN)
% Manuel Luque : manuel.luque27@gmail.com
% 6 avril 2003
\definecolor{Bluea}{cmyk}{.2,0,0,0}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\def\manometre{%
\rput(0,0){%
\psline[doubleline=true,doublesep=0.12,linearc=0.2](0,0)(2,0)(2,-2)
\pscircle[doubleline=true,fillstyle=solid](0,0){0.9}
\psarc(0,0){0.65}{-60}{240}
\multido{\i=-60+30}{11}{\psline(0.65;\i)(0.45;\i)}
\psline[arrowscale=2,linewidth=2\pslinewidth]{->}(0.5;-20)(0.65;160)
\pscircle[fillstyle=solid]{0.1}}}
\def\Bouchon{%
\psellipse[linewidth=1.5\pslinewidth](0,0.2)(0.6,0.1)
\begingroup
\psset{fillstyle=solid,fillcolor=lightgray}
\psellipse(0,-0.4)(0.32,0.1)
\pspolygon(-0.5,0.5)(-0.32,-0.4)(0.32,-0.4)(0.5,0.5)
\psellipse[linestyle=none,dimen=outer,linewidth=0.07](0,-0.4)(0.32,0.1)
\psellipse(0,0.5)(0.5,0.1)
\endgroup
\psellipticarc[linewidth=1.5\pslinewidth](0,0.2)(0.6,0.1){180}{0}
\psline[doubleline=true,doublesep=0.12,doublecolor=white](-0.2,0.5)(-0.2,0.6)
\psline[doubleline=true,dimen=outer,doublesep=0.05,doublecolor=red](0.2,0.5)(0.2,1)}
\newcommand\erlen{%
\begin{psclip}{%
\pspolygon[linestyle=none,linearc=0.2](-0.6,3.2)(-0.4,3)(-0.4,2)(-1.2,0)(1.2,0)(0.4,2)%
(0.4,3)(0.6,3.2)}
\psclip{\pscustom[linecolor=cyan,fillstyle=solid,fillcolor=Bluea]{%
\pscurve(-2,0.9)(-1.75,1)(-1.5,0.9)(-1.25,1)(-1,0.9)
(-0.75,1)(-0.5,0.9)(-0.25,1)(0,0.9)
(0.25,1)(0.5,0.9)(0.75,1)(1,0.9)
(1.25,1)(1.5,0.9)(1.75,1)(2,0.9)
\psline(2,0.9)(2,-1)(-2,-1)(-2,0.9)}}
\BILLES
\endpsclip
\end{psclip}
\psline[linearc=0.2](-0.6,3.2)(-0.4,3)(-0.4,2)(-1.2,0)(1.2,0)(0.4,2)
\psline[linearc=0.05](0.4,2)(0.4,2.4)(1.4,2.4)
\psline[linearc=0.05](1.4,2.6)(0.4,2.6)(0.4,3)(0.6,3.2)}
\def\thermometre{%
\pspolygon[linearc=0.05,fillstyle=solid,fillcolor=red](0.05,3)(0.05,-1.2)
(0.15,-1.2)(0.15,-1.8)(-0.15,-1.8)(-0.15,-1.2)(-0.05,-1.2)(-0.05,3)
\psframe[linearc=0.05,fillstyle=solid](-0.05,1)(0.05,3)}
\makeatletter
\newdimen\BX
\newdimen\BY
\newdimen\RAYONBULLE
\makeatletter
\newcommand{\BILLES}[1][50]{%
\multido{\IBULLE=1+1}{#1}{%
\setrandim{\BX}{-1.5\psunit}{1.5\psunit}
\setrandim{\BY}{0\psunit}{1\psunit}
\pst@dimh=\BY
\setrandim{\RAYONBULLE}{0.01\psunit}{0.1\psunit}
\ifdim\BY>2\psunit \multiply \RAYONBULLE by 3
\else
\ifdim\BY < 2\psunit \ifdim\BY >1\psunit \multiply \RAYONBULLE by 2\fi
\else
\multiply \RAYONBULLE by 1
\fi
\fi
\rput(0,0){%
\pscircle[style=BilleThreeD](\BX,\BY){\RAYONBULLE}}}}
\newpsstyle{BilleThreeD}{linestyle=none,fillstyle=gradient,gradmidpoint=0,gradend=white,GradientCircle}
\pagestyle{empty}
\begin{document}
\begin{center}
\begin{pspicture}(-5,0)(5,6)
\rput(-2.2,4){\manometre}
\erlen
\rput(0.2,3){\thermometre}
\rput(0,3){\Bouchon}
\psline{->}(1.5,2.5)(2.5,2.5)
%\uput[0](2.5,2.5){vers trompe \`a eau}
\end{pspicture}
\end{center}
\end{document}
\usepackage{pst-grad,multido}%
\input{random.tex} % From Donald Arseneau (on macros/generic on CTAN)
% Manuel Luque : manuel.luque27@gmail.com
% 6 avril 2003
\definecolor{Bluea}{cmyk}{.2,0,0,0}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\def\manometre{%
\rput(0,0){%
\psline[doubleline=true,doublesep=0.12,linearc=0.2](0,0)(2,0)(2,-2)
\pscircle[doubleline=true,fillstyle=solid](0,0){0.9}
\psarc(0,0){0.65}{-60}{240}
\multido{\i=-60+30}{11}{\psline(0.65;\i)(0.45;\i)}
\psline[arrowscale=2,linewidth=2\pslinewidth]{->}(0.5;-20)(0.65;160)
\pscircle[fillstyle=solid]{0.1}}}
\def\Bouchon{%
\psellipse[linewidth=1.5\pslinewidth](0,0.2)(0.6,0.1)
\begingroup
\psset{fillstyle=solid,fillcolor=lightgray}
\psellipse(0,-0.4)(0.32,0.1)
\pspolygon(-0.5,0.5)(-0.32,-0.4)(0.32,-0.4)(0.5,0.5)
\psellipse[linestyle=none,dimen=outer,linewidth=0.07](0,-0.4)(0.32,0.1)
\psellipse(0,0.5)(0.5,0.1)
\endgroup
\psellipticarc[linewidth=1.5\pslinewidth](0,0.2)(0.6,0.1){180}{0}
\psline[doubleline=true,doublesep=0.12,doublecolor=white](-0.2,0.5)(-0.2,0.6)
\psline[doubleline=true,dimen=outer,doublesep=0.05,doublecolor=red](0.2,0.5)(0.2,1)}
\newcommand\erlen{%
\begin{psclip}{%
\pspolygon[linestyle=none,linearc=0.2](-0.6,3.2)(-0.4,3)(-0.4,2)(-1.2,0)(1.2,0)(0.4,2)%
(0.4,3)(0.6,3.2)}
\psclip{\pscustom[linecolor=cyan,fillstyle=solid,fillcolor=Bluea]{%
\pscurve(-2,0.9)(-1.75,1)(-1.5,0.9)(-1.25,1)(-1,0.9)
(-0.75,1)(-0.5,0.9)(-0.25,1)(0,0.9)
(0.25,1)(0.5,0.9)(0.75,1)(1,0.9)
(1.25,1)(1.5,0.9)(1.75,1)(2,0.9)
\psline(2,0.9)(2,-1)(-2,-1)(-2,0.9)}}
\BILLES
\endpsclip
\end{psclip}
\psline[linearc=0.2](-0.6,3.2)(-0.4,3)(-0.4,2)(-1.2,0)(1.2,0)(0.4,2)
\psline[linearc=0.05](0.4,2)(0.4,2.4)(1.4,2.4)
\psline[linearc=0.05](1.4,2.6)(0.4,2.6)(0.4,3)(0.6,3.2)}
\def\thermometre{%
\pspolygon[linearc=0.05,fillstyle=solid,fillcolor=red](0.05,3)(0.05,-1.2)
(0.15,-1.2)(0.15,-1.8)(-0.15,-1.8)(-0.15,-1.2)(-0.05,-1.2)(-0.05,3)
\psframe[linearc=0.05,fillstyle=solid](-0.05,1)(0.05,3)}
\makeatletter
\newdimen\BX
\newdimen\BY
\newdimen\RAYONBULLE
\makeatletter
\newcommand{\BILLES}[1][50]{%
\multido{\IBULLE=1+1}{#1}{%
\setrandim{\BX}{-1.5\psunit}{1.5\psunit}
\setrandim{\BY}{0\psunit}{1\psunit}
\pst@dimh=\BY
\setrandim{\RAYONBULLE}{0.01\psunit}{0.1\psunit}
\ifdim\BY>2\psunit \multiply \RAYONBULLE by 3
\else
\ifdim\BY < 2\psunit \ifdim\BY >1\psunit \multiply \RAYONBULLE by 2\fi
\else
\multiply \RAYONBULLE by 1
\fi
\fi
\rput(0,0){%
\pscircle[style=BilleThreeD](\BX,\BY){\RAYONBULLE}}}}
\newpsstyle{BilleThreeD}{linestyle=none,fillstyle=gradient,gradmidpoint=0,gradend=white,GradientCircle}
\pagestyle{empty}
\begin{document}
\begin{center}
\begin{pspicture}(-5,0)(5,6)
\rput(-2.2,4){\manometre}
\erlen
\rput(0.2,3){\thermometre}
\rput(0,3){\Bouchon}
\psline{->}(1.5,2.5)(2.5,2.5)
%\uput[0](2.5,2.5){vers trompe \`a eau}
\end{pspicture}
\end{center}
\end{document}
Illustration de la loi de Mariotte (Boyle)
\documentclass{article}
\usepackage[paperwidth=15cm,paperheight=4cm,hmargin={0cm,0cm},vmargin={0cm,0cm},dvips]{geometry}
\usepackage{pstricks,multido}%
\input{random.tex} % From Donald Arseneau (on macros/generic on CTAN)
\def\syringe#1{% position piston -3.5<->-0.5
\psclip{\psframe(#1,-1)(0.8,1)}
\RandomMolecule{400}{#1}
\endpsclip
\psline[doubleline=true,doublesep=2mm](1,0)(3.1,0)
\rput(!#1 -2 sub 0){\pscircle[doubleline=true](-6.5,0){0.6}
\psframe[fillstyle=solid,fillcolor=yellow!10](-6,-0.5)(-2,0.5)
\psline[linewidth=2mm](-2,-1)(-2,1)}%
\psframe(-4,1)(0.8,-1)
\multido{\n=-3.5+0.5}{9}{%
\psline(\n,1)(\n,0.7)}
\pscircle[doubleline=true,fillstyle=solid](4,0){1}
\psarc(4,0){0.65}{-60}{240}
\multido{\i=-60+30}{11}{\rput(4,0){\psline(0.65;\i)(0.45;\i)}}
\rput{!337.5 #1 45 mul sub}(4,0){\psline[arrowscale=2,linewidth=2\pslinewidth]{->}(-0.5,0)(0.65,0)}
\psframe[fillstyle=solid](-4.1,-1.2)(-4,1.2)
\psline(0.8,1)(1,0.1)(1,-0.1)(0.8,-1)
}%
% idée empruntée à Denis Girou
\newdimen\X
\newdimen\Y
\def\RandomMolecule#1#2{%
\multido{\i=1+1}{#1}{%
\setrandim\X{#2 pt}{1pt}
\setrandim\Y{-1pt}{1pt}
\pscircle*[linecolor=blue](\pointless\X,\pointless\Y){1pt}}}
\pagestyle{empty}
\begin{document}
\begin{center}
\multido{\r=-3.5+0.1}{32}{%
\begin{pspicture}(-9,-2)(6,2)
\psframe(-9,-2)(6,2)
\syringe{\r}
\end{pspicture}\newpage}
\multido{\r=-0.3+-0.1}{32}{%
\begin{pspicture}(-9,-2)(6,2)
\psframe(-9,-2)(6,2)
\syringe{\r}
\end{pspicture}\newpage}
\end{center}
\end{document}
mardi 19 avril 2016
Cercle chromatique des espaces HSB / HSV
Référence : https://fr.wikipedia.org/wiki/Teinte_saturation_lumi%C3%A8re
\documentclass{article}
\usepackage[garamond]{mathdesign}
\usepackage{pstricks,multido}
% Manuel Luque
\date{19 avril 2016}
\begin{document}
\begin{center}
\begin{pspicture}[showgrid=false](-6,-6)(6,6)
\psframe*(-6,-6)(6,6)
\pstVerb{/Unit {28.45274 mul} bind def /radius 4 def /Radius {radius Unit} def
/CoordM {/iA exch def radius iA cos mul radius iA sin mul} def}%
\multido{\i=0+30}{12}{\white %
\pstVerb{/M0 {radius \i\space cos mul radius \i\space sin mul} def /M1 {radius 0.5 add \i\space cos mul radius 0.5 add \i\space sin mul} def }%
\psline[linecolor=white](!M0)(!M1)%
\uput{0.05}[\i](!M1){\small\i$^{\mathrm{o}}$}}%
\uput{1}[0](!radius 0){\textcolor{red}{\textbf{R}}}
\uput{1}[60](!60 CoordM){\textcolor{yellow}{\textbf{Y}}}
\uput{1}[120](!120 CoordM){\textcolor{green}{\textbf{G}}}
\uput{1.2}[180](!180 CoordM){\textcolor{cyan}{\textbf{C}}}
\uput{1}[240](!240 CoordM){\textcolor{blue}{\textbf{B}}}
\uput{1}[300](!300 CoordM){\textcolor{magenta}{\textbf{M}}}
\pscustom{
\code{%
/secteur {newpath
0 0 moveto
Radius i 1 sub cos mul
0 0 Radius i 1 sub i 1 add arc
closepath
} def
0 1 360 {/i exch def /HUE i 360 div def
secteur
HUE 1 1 sethsbcolor fill} for
}
}%
\rput(0,-5.5){\white Cercle chromatique des espaces HSB / HSV}
\end{pspicture}
\end{center}
\end{document}
dimanche 17 avril 2016
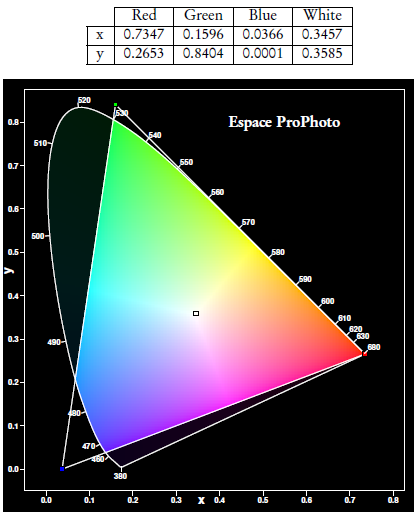
Diagramme de chromaticité, gamut : package pst-cie
En utilisant les données de la Commission Internationale d’Éclairage (CIE XYZ 1931 et CIE XYZ 1964), le package‘pst-cie’ se propose de représenter le gamut de couleurs et/ou le diagramme de chromaticité pour différents espaces de couleurs. Les pages web consacrées aux études et représentations des diagrammes de chromaticité et des gamuts sont très nombreuses et il est difficile d’en distinguer une plutôt qu’une autre, cependant en voici qui m’ont bien plu : celles de Frédéric Legrand :
consacrées à la colorimétrie, et celles de Daniel Metz :
Yu-Sung Chang a réalisé avec le logiciel Mathematica une version interactive de toute beauté :
comme je ne possède pas ce logiciel, j’ai essayé de faire à peu près la même chose avec PSTricks, ou tout au moins ayant presque les mêmes fonctionnalités.
Les matrices de conversion utilisées dans le package ont été calculées par Bruce Justin Lindbloom :
La commande s’écrit \psChromaticityDiagram[options], les options sont décrites dans la documentation(incluse dans l'archive) :
Quelques images obtenues avec ce package et extraites de la documentation :
Pour l'animation avec le package animate, rajoutez ces quelques lignes dans le fichier de la documentation :
\begin{center}
\begin{animateinline}[controls,palindrome,
begin={\begin{pspicture}(-1,-1)(8.5,11)},
end={\end{pspicture}}]{2}% 2 images/s
\multiframe{10}{n=1.0+-0.1}{%
\psChromaticityDiagram[contrast=\n,primaries=false]
\rput(5.5,8){\white \textbf{Espace sRGB}}
\rput(4,10){\tabsRGB}
}
\end{animateinline}
\end{center}
dimanche 10 avril 2016
Rayonnement du corps noir : package pst-t2rgb
Ce package permet d'afficher la couleur du rayonnement du corps noir à une température donnée dans une figure quelconque ou sur une plage de température [T1,T2].
Il offre la possibilité de choisir entre deux méthodes :
Couleur de quelques étoiles :
Les packages et leurs documentations sont dans l'archive :
pst-t2rgb.zip
Il offre la possibilité de choisir entre deux méthodes :
- celle modélisée par Tanner Helland et améliorée par Neil Bartlett ;
- celle utilisant les valeurs tabulées de la Commission Internationale de l'Éclairage (CIE 1931), la procédure de calculs est détaillée dans la documentation.
Couleur de quelques étoiles :
Bételgeuse
Rigel
Sun
Une animation illustrant la loi de Planck, utilisant les 2 packages : pst-t2rgb et pst-xspectrum.
pst-t2rgb.zip
Inscription à :
Commentaires (Atom)