Ce message et le précédent sont une tentative de vérification d'une affirmation contenue dans un article du dossier du magazine `Pour la Science' n°91 d'Avril-Juin 2016'. Cet article est intitulé ``Mayonnaise et élections américaines'' et a pour sujet, en réalité, les équations différentielles stochastiques. Dans l'encadré de la page 104, on trouve cette illustration avec l'affirmation que je me proposais de vérifier en utilisant les équations différentielles ordinaires.
À vrai dire, je ne pense pas qu'on puisse appeler cela une vérification, car la méthode de résolution numérique induit à chaque pas une erreur qui s'ajoute aux précédentes(elles ne se compensent pas) et sur un grand intervalle de temps vérifier que les ressorts de rang pair et de rang impair restent parallèles est illusoire, on peut tout au moins, si la précision du logiciel est grande, en avoir un aperçu : est-ce la cas de Postscript ?
En tout cas voici pour 5 oscillateurs couplés par 4 ressorts, cependant la simulation serait plus concluante avec un grand nombre de ressorts. Comme l'indique Nils Berglund dans l'article :
http://images.math.cnrs.fr/Qu-est-ce-qu-une-Equation-aux-Derivees-Partielles-Stochastique.html
« Au lieu de chercher à résoudre le système de N équations différentielles ordinaires (EDO) décrivant le mouvement des N billes, on peut essayer de décrire directement l’évolution de la courbe d’interpolation. L’interaction de chaque bille avec ses voisines se traduit alors dans l’équation par un terme dépendant de la courbure. L’équation qui en résulte est une équation aux dérivées partielles (EDP), appelée équation d’Allen—Cahn. »
Mais ça je ne sais pas le faire.
Voici le code permettant d'obtenir les images pour créer un GIf animé ou une vidéo :
\documentclass{article}
\usepackage[paperwidth=14cm,paperheight=10cm,hmargin={0cm,0cm},vmargin={0cm,0cm},dvips]{geometry}
\usepackage{pst-ode,pst-ressort,multido}
\pagestyle{empty}
\begin{document}
\def\mobileA{\pscustom[fillstyle=solid,fillcolor=red,unit=0.2]{\psline(-0.5,0.1)(-2,0.1)(-2,1)(2,1)(2,0.1)
\psarcn(0,0.1){0.5}{0}{180}
\moveto(-0.2,0.1)
\psarc(0,0.1){0.2}{180}{360}
\psline(0.2,0.1)(-0.2,0.1)}}
\def\mobileB{\psframe[fillstyle=solid,fillcolor=yellow,unit=0.2](-2,-0.5)(2,0.5)}
\def\mobileC{\pscustom[fillstyle=solid,fillcolor=red,unit=0.2]{\psline(0.5,-0.1)(2,-0.1)(2,-1)(-2,-1)(-2,-0.1)(-0.5,-0.1)
\psarcn(0,-0.1){0.5}{180}{0}
\moveto(0.2,-0.1)
\psarc(0,-0.1){0.2}{0}{180}
\psline(-0.2,-0.1)(0.2,-0.1)}}
% 4 mobiles
% 0 1 2 3 4 5 6 7 8 9
% x1 x2 x3 x4 x5 x'1 x'2 x'3 x'4 x'5
\def\CinqOscillateurs{x[5]|x[6]|x[7]|x[8]|x[9]|km*(x[1]-x[0])*(1-L0/sqrt(distance^2+(x[1]-x[0])^2))|%
-km*(x[1]-x[0])*(1-L0/sqrt(distance^2+(x[1]-x[0])^2))+km*(x[2]-x[1])*(1-L0/sqrt(distance^2+(x[2]-x[1])^2))|%
-km*(x[2]-x[1])*(1-L0/sqrt(distance^2+(x[2]-x[1])^2))+km*(x[3]-x[2])*(1-L0/sqrt(distance^2+(x[3]-x[2])^2))|%
-km*(x[3]-x[2])*(1-L0/sqrt(distance^2+(x[3]-x[2])^2))+km*(x[4]-x[3])*(1-L0/sqrt(distance^2+(x[4]-x[3])^2))|%
-km*(x[4]-x[3])*(1-L0/sqrt(distance^2+(x[4]-x[3])^2))}
\def\initCond{x1 x2 x3 x4 x5 vx1 vx2 vx3 vx4 vx5}
\begin{center}
\multido{\i=0+1}{500}{%
\begin{pspicture}(-7,-5)(7,5)
\pstVerb{/x1 3 def
/vx1 0 def
/x2 -3 def
/vx2 0 def
/x3 3 def
/vx3 0 def
/x4 -3 def
/vx4 0 def
/x5 3 def
/vx5 0 def
% k/m = km =4pi^2 = 39.4784176
/km 39.4784176 def
/L0 1 def
/distance 2 def
}%
\pstODEsolve[algebraic]{mobile01234}{0 1 2 3 4}{0}{10}{1000}{\initCond}{\CinqOscillateurs}
\pstVerb{
/posX1 [0 5 [mobile01234] length 5 sub {/i exch def
[mobile01234] i get} for
]def
/posX2 [0 5 [mobile01234] length 5 sub {/i exch def
[mobile01234] i 1 add get} for
]def
/posX3 [0 5 [mobile01234] length 5 sub {/i exch def
[mobile01234] i 2 add get} for
]def
/posX4 [0 5 [mobile01234] length 5 sub {/i exch def
[mobile01234] i 3 add get} for
]def
/posX5 [0 5 [mobile01234] length 5 sub {/i exch def
[mobile01234] i 4 add get} for
]def }%
\psframe*[linecolor=cyan!20](-7,-5)(7,5)
\psline[linewidth=0.05](-7,4.1)(7,4.1)
\psline[linewidth=0.05](-7,-4.1)(7,-4.1)
\psline[linewidth=0.05](-7,2)(7,2)
\psline[linewidth=0.05](-7,-2)(7,-2)
\psline[linewidth=0.05](-7,0)(7,0)
\rput(!posX1 \i\space get 4){\mobileA}
\rput(!posX2 \i\space get 2){\mobileB}
\rput(!posX3 \i\space get 0){\mobileB}
\rput(!posX4 \i\space get -2){\mobileB}
\rput(!posX5 \i\space get -4){\mobileC}
\psRessort[N=20,li=0.5,R=0.15,alpha=20,dl=0.4,linecolor=blue]{*-*}(!posX1 \i\space get 4)(!posX2 \i\space get 2)
\psRessort[N=20,li=0.5,R=0.15,alpha=20,dl=0.4,linecolor=blue]{*-*}(!posX2 \i\space get 2)(!posX3 \i\space get 0)
\psRessort[N=20,li=0.5,R=0.15,alpha=20,dl=0.4,linecolor=blue]{*-*}(!posX3 \i\space get 0)(!posX4 \i\space get -2)
\psRessort[N=20,li=0.5,R=0.15,alpha=20,dl=0.4,linecolor=blue]{*-*}(!posX4 \i\space get -2)(!posX5 \i\space get -4)
\end{pspicture}\newpage}
\end{center}
\end{document}

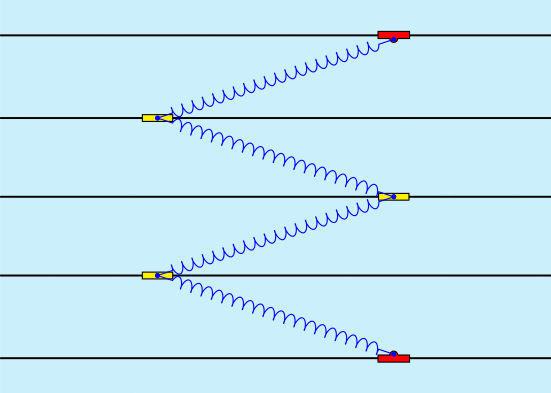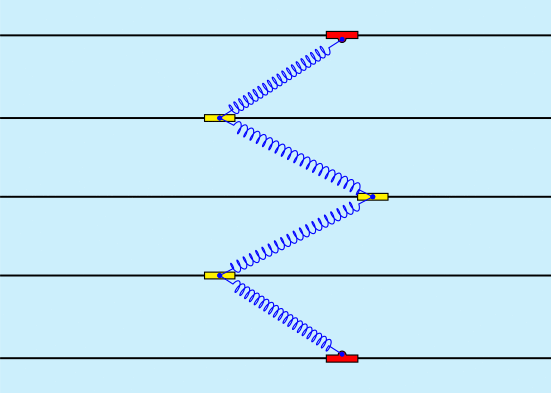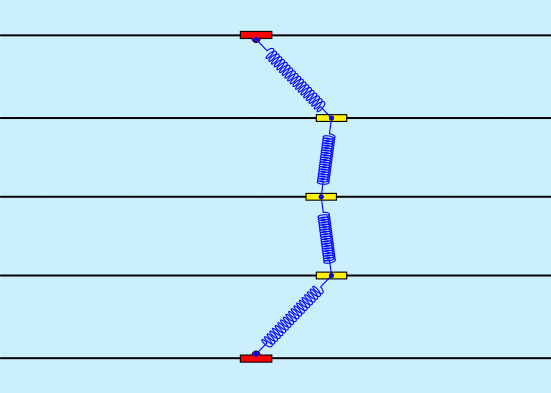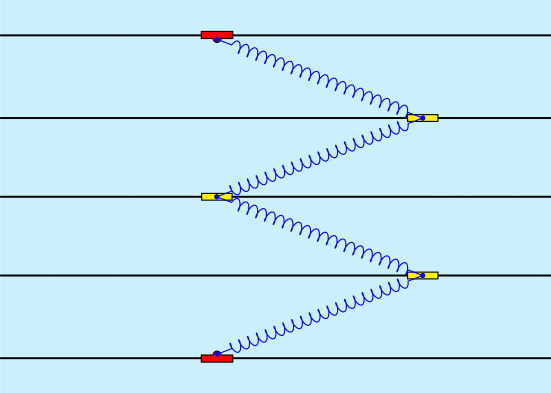
Aucun commentaire:
Enregistrer un commentaire